Introduction
Several days ago SAP released "SAP HANA Cloud's Vector Engine" which is essentially a database that stores finite dimensional vectors that represent real worlds objects. Furthermore these kind of databases have built-in functions in order to calculate certain relations between the stored vectors. The vectors are the result of a so called embedding, which means that each real worlds object is "embedded" into a finite dimensional vector space in a certain way. The embedding itself depends on the purpose of the usage of the vectors and is not uniquely determined. For example all orthogonal transformations preserve the inner structure of the embedding. (Note that this is not an embedding in the mathematical sense, which is a one to one differentiable mapping between vector spaces that is locally invertable).
Example
We want to classify incoming documents. Assume we have two classes of documents: Invoices and delivery notes. Assume furthermore you had already 1000 delivery notes and 1000 invoices. Then we could try to find the 10 types (words) in these documents that are separating these two classes in the best way. In this example one can guess these words: E.g. "Invoice, Amount, Quantity, Delivery Note, Delivery Date...". Let's say we find 8 words. Then we count for each document how often the word appears in the document. We normalize this number by the count of words in the document, since we don't want that large documents get larger weight than small ones. This defines an embedding into an 8-dimensional vector space. The vectors are called training vectors. Actually they are comparsion examples. If we now get a new document and want the computer to decide if it is an invoice or a delivery note we calculate the vector representation of the document as above described. Then we calculate the euclidean distances to the 2000 training vectors. One distance will be the smallest (hopefully it is one or at least several with the same class, otherwise we cannot decide). The class of this closest vector will be the class of our new test vector. This ML model is called KNN (k-nearest neighbor, in our case 1-nearest neighbor).
Note: The euclidean distance is defined in the following way. Let v1 and v2 be two vectors. Calculate
v_diff = v1-v2.
The euclidean distance of v1 and v2 is defined as
||v_diff||
where
||.|| = sqrt(<.,.>)
and <.,.> is the inner product in R^n, i.e.
<v,w> = v1*w1+ ... + vn*wn.
Problem
In the above example we had to calculate 2000 difference vectors and 2000 inner products of 8-dim. vectors. This can be done easily in ABAP and is not very time consuming. Now assume we had 10.000.000 300-dimensional vectors as comparison vectors. Then we had to calculate 10.000.000 inner products of 300-dimensional vectors which are 300 * 10.000.000 = 3*10^9 multiplications of floating point variables. This would be very time consuming in an ABAP program. Numbers of this size can arise when we e.g. consider a Word2Vec embedding of a large corpus. This kind of embedding is done in order to do similarity searches. For these "large" embeddings we need a vector database which is able to calculate the inner products in a efficient way.
Unfortunately the SAP HANA Cloud's Vector DB is not available on SAP HANA on-premise. Thus we cannot use the functions of the vector DB. But the PAL (Predictive Analysis Libary) is available and the KNN-algorithm is available in PAL:
Solution
Although we do not have a classification problem we can use the KNN algorithm in order to calculate our inner products and find the nearest neighhbor. We simply ignore the capability of KNN to classify and assign always the same class to our training (comparison) vectors. Our class is always "100". As a result we get the k-nearest neighbors and the distances. The following program calculates nearest neighbors of 1000 test vectors to randomly generated 10.000.000 8-dimensional vectors in a couple of seconds. This code can be directly applied to a e.g. Word2Vec embedding in oder to create a similarity search engine. It was a good idea to encapsulate this code into a re-usable method.
*&---------------------------------------------------------------------*
*& Report ZZZ_TEST_KNN
*&---------------------------------------------------------------------*
*&
*&---------------------------------------------------------------------*
REPORT zzz_test_knn.
DATA: ls_train TYPE zcl_knn=>ty_train,
lt_train TYPE zcl_knn=>tt_train,
ls_test TYPE zcl_knn=>ty_test,
lt_test TYPE zcl_knn=>tt_test,
ls_params TYPE zcl_knn=>ty_params,
lt_params TYPE zcl_knn=>tt_params,
ls_result TYPE zcl_knn=>ty_result,
lt_result TYPE zcl_knn=>tt_result,
ls_stat TYPE zcl_knn=>ty_stat,
lt_stat TYPE zcl_knn=>tt_stat.
**Training data records
*ls_train-id1 = 1.
*ls_train-x1 = '1.0'.
*ls_train-x2 = '1.0'.
*ls_train-x3 = '1.0'.
*ls_train-type = 100.
*APPEND ls_train TO lt_train.
*
*ls_train-id1 = 2.
*ls_train-x1 = '2.0'.
*ls_train-x2 = '3.0'.
*ls_train-x3 = '4.0'.
*ls_train-type = 200.
*APPEND ls_train TO lt_train.
*
*ls_train-id1 = 3.
*ls_train-x1 = '5.0'.
*ls_train-x2 = '6.0'.
*ls_train-x3 = '7.0'.
*ls_train-type = 300.
*APPEND ls_train TO lt_train.
*
**Test record
*ls_test-id2 = 1.
*ls_test-x1 = '1.0'.
*ls_test-x2 = '1.0'.
*ls_test-x3 = '0.5'.
*APPEND ls_test TO lt_test.
DATA(lo_random) = cl_abap_random_float=>create( ).
DO 1000000 TIMES.
ls_train-id1 = sy-index.
ls_train-x1 = lo_random->get_next( ).
ls_train-x2 = lo_random->get_next( ).
ls_train-x3 = lo_random->get_next( ).
ls_train-x5 = lo_random->get_next( ).
ls_train-x6 = lo_random->get_next( ).
ls_train-x7 = lo_random->get_next( ).
ls_train-x8 = lo_random->get_next( ).
ls_train-type = 100.
APPEND ls_train TO lt_train.
ENDDO.
*Test record
ls_test-id2 = 1.
ls_test-x1 = '0.5'.
ls_test-x2 = '0.5'.
ls_test-x3 = '0.5'.
ls_test-x4 = '0.5'.
ls_test-x5 = '1.5'.
ls_test-x6 = '5.5'.
ls_test-x7 = '3.5'.
ls_test-x8 = '9.5'.
APPEND ls_test TO lt_test.
*DO 1000 TIMES.
* ls_test-id2 = sy-index.
* ls_test-x1 = lo_random->get_next( ).
* ls_test-x2 = lo_random->get_next( ).
* ls_test-x3 = lo_random->get_next( ).
* ls_test-x5 = lo_random->get_next( ).
* ls_test-x6 = lo_random->get_next( ).
* ls_test-x7 = lo_random->get_next( ).
* ls_test-x8 = lo_random->get_next( ).
* APPEND ls_test TO lt_test.
*ENDDO.
ls_params-name = 'METHOD'.
ls_params-intargs = 1. "K-d-tree
APPEND ls_params TO lt_params.
ls_params-name = 'DEPENDENT_VARIABLE'.
ls_params-stringargs = 'TYPE'.
APPEND ls_params TO lt_params.
ls_params-name = 'K_NEAREST_NEIGHBOURS'.
ls_params-intargs = 1000.
APPEND ls_params TO lt_params.
BREAK-POINT.
zcl_knn=>do_knn(
EXPORTING
it_train = lt_train
it_test = lt_test
it_params = lt_params
IMPORTING
et_result = lt_result
et_stat = lt_stat ).
BREAK-POINT.
The program uses this class:
CLASS zcl_knn DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
INTERFACES if_amdp_marker_hdb .
TYPES: BEGIN OF ty_train,
id1 TYPE i,
x1 TYPE float,
x2 TYPE float,
x3 TYPE float,
x4 TYPE float,
x5 TYPE float,
x6 TYPE float,
x7 TYPE float,
x8 TYPE float,
type TYPE int4,
END OF ty_train,
tt_train TYPE STANDARD TABLE OF ty_train,
BEGIN OF ty_test,
id2 TYPE i,
x1 TYPE float,
x2 TYPE float,
x3 TYPE float,
x4 TYPE float,
x5 TYPE float,
x6 TYPE float,
x7 TYPE float,
x8 TYPE float,
END OF ty_test,
tt_test TYPE STANDARD TABLE OF ty_test,
BEGIN OF ty_params,
name TYPE c LENGTH 60,
intargs TYPE i,
doubleargs TYPE float,
stringargs TYPE c LENGTH 100,
END OF ty_params,
tt_params TYPE STANDARD TABLE OF ty_params,
BEGIN OF ty_result,
id2 TYPE i,
target TYPE char10,
END OF ty_result,
tt_result TYPE STANDARD TABLE OF ty_result,
BEGIN OF ty_stat,
test_id2 TYPE i,
k TYPE i,
train_id1 TYPE i,
distance TYPE float,
END OF ty_stat,
tt_stat TYPE STANDARD TABLE OF ty_stat.
CLASS-METHODS: do_knn
IMPORTING
VALUE(it_train) TYPE tt_train
VALUE(it_test) TYPE tt_test
VALUE(it_params) TYPE tt_params
EXPORTING
VALUE(et_result) TYPE tt_result
VALUE(et_stat) TYPE tt_stat.
PROTECTED SECTION.
PRIVATE SECTION.
ENDCLASS.
CLASS ZCL_KNN IMPLEMENTATION.
* <SIGNATURE>---------------------------------------------------------------------------------------+
* | Static Public Method ZCL_KNN=>DO_KNN
* +-------------------------------------------------------------------------------------------------+
* | [--->] IT_TRAIN TYPE TT_TRAIN
* | [--->] IT_TEST TYPE TT_TEST
* | [--->] IT_PARAMS TYPE TT_PARAMS
* | [<---] ET_RESULT TYPE TT_RESULT
* | [<---] ET_STAT TYPE TT_STAT
* +--------------------------------------------------------------------------------------</SIGNATURE>
METHOD do_knn BY DATABASE PROCEDURE FOR HDB LANGUAGE SQLSCRIPT.
CALL _SYS_AFL.PAL_KNN(:it_train, :it_test, :it_params, et_result, et_stat);
ENDMETHOD.
ENDCLASS.
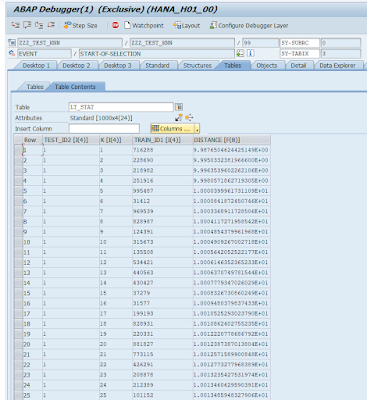
The result vectors:
Notes:
1. It is a good idea if the reader convinces himself that this program works correctly by applying it to small example (use the commented code).
2. The results can be seen in debugger.
3. The result of interest is not in the table "lt_result" but in the table "lt_stat".
4. By using more then one class this code represents an example on "how to use PAL KNN by AMDP".
5. Instead of using the euclidean distance in KNN one can use cosine similarity. Furthermore by calculating the distance to the null vector it is possible to calculate the length of the vectors. Having the length and the cosine similarity an easy calculation gives the inner product. Thus we can also calculate the inner products of the vectors.
6. The reader may try other distances than the euclidean. Available are:
1: Manhattan distance
2: Euclidean distance
3: Minkowski distance
4: Chebyshev distance
6: Cosine distance
7. PAL KNN allows brute force searching or KD-tree searching.Since the KD-tree has to be built in advance a runtime advantage can arise only for a larger amount of test vectors.
Open question: Is it possible to store the KD-tree in order to re-use it in susequent calls?
No comments:
Post a Comment